Công thức lượng giác đã rất quen thuộc, gần gũi với học sinh lớp 9 lớp 10 lớp 11 trong các kỳ thi quan trọng. Với số lượng công thức rất nhiều, việc học thuộc là không hề đơn giản, đòi hỏi cần sự kiên nhẫn và những bí kíp để ghi nhớ dễ dàng hơn.
Để giúp các em học sinh tiếp thu công thức lượng giác nhanh chóng. Bài viết dưới đây Wikikienthuc.com sẽ bật mí thông tin chi tiết nhất về mảng kiến thức này.
Nội dung chính:
- 1 Công thức lượng giác là gì?
- 2 Bảng công thức lượng giác cơ bản
- 3 Mẹo học thuộc công thức lượng giác nhanh chóng nhất
- 3.1 1. Học thuộc công thức cộng lượng giác
- 3.2 2. Học thuộc công thức lượng giác đặc biệt
- 3.3 3. Học thuộc công thức lượng giác nhân ba
- 3.4 4. Học thuộc công thức lượng giác gấp đôi
- 3.5 5. Học thuộc công thức lượng giác biến đổi tổng thành tích nhanh chóng
- 3.6 6. Học thuộc công thức lượng giác biến đổi tích thành tổng
Công thức lượng giác là gì?
Lượng giác có tên tiếng Anh là Trigonometry – “tam giác” và “đo lường”. Đây là một nhánh của toán học để tìm hiểu về hình tam giác cùng những cạnh của chúng với vai trò hàm số lượng giác. Hàm số lượng giác sẽ diễn ra mối liên kết, áp dụng dễ dàng vào việc học hiện tượng có chu kỳ – ví dụ như sóng âm.
Công thức lượng giác đã được sinh ra từ thế kỷ 3 trước công nguyên. Ban đầu, đây chỉ là một nhánh của toán hình, chuyên dùng để nghiên cứu thiên văn. Tuy nhiên sau này lượng giác đã phát triển và trở thành một phần không thể thiếu trong quá trình khám phá, tìm hiểu Toán học thế giới.
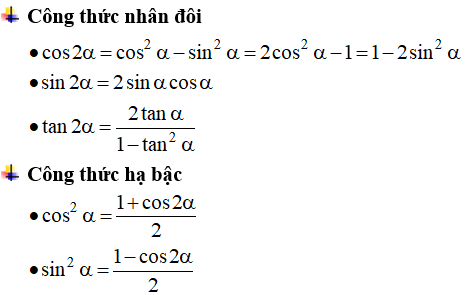
Xem thêm: Danh sách các hằng đẳng thức mở rộng cơ bản và nâng cao
Bảng công thức lượng giác cơ bản
Khi bắt đầu vào chương trình THPT, các em học sinh sẽ được tiếp cận với lượng giác. Đây thực sự là một trong những mảng khó nhất của Toán học – với số lượng công thức cần ghi nhớ dày đặc và đa dạng. Một số công thức cơ bản bạn có thể tham khảo và học thuộc đó là:
Công thức lượng giác cơ bản
Dưới đây là danh sách các công thức lượng giác cơ bản chi tiết nhất. Các em có thể tham khảo qua các công thức sau đây:
1. Công thức cộng lượng giác
- sin (a ± b) = sin a.cos b ± cos a.sin b
- cos (a + b) = cos a.cos b – sin a.sin b
- cos (a – b) = cos a.cos b + sin a.sin b
Mẹo ghi nhớ công thức cộng: với sin => sin cos cos sin, với cos => cos cos sin sin dấu trừ. Với tan: tan nọ tan kia chia cho mẫu trừ tan tan.
2. Công thức kết hợp các cung trên đường tròn lượng giác
Công thức hai góc đối nhau:
- cos (-x) = cos x
- sin (-x) = -sin x
- tan (-x) = -tan x
- cot (-x) = -cot x
Công thức hai góc bù nhau:
- sin (π – x) = sin x
- cos (π – x) = -cos x
- tan (π – x) = -tan x
- cot (π – x) = -cot x
Công thức hai góc phụ nhau:
- sin (π/2 – x) = cos x
- cos (π/2 – x) = sin x
- tan (π/2 – x) = cot x
- cot (π/2 – x) = tan x
Công thức hai góc hơn kém π:
- sin (π + x) = -sin x
- cos (π + x) = -cos x
- tan (π + x) = tan x
- cot (π + x) = cot x
Công thức hai góc hơn kém π/2:
- sin (π/2 + x) = cos x
- cos (π/2 + x) = -sin x
- tan (π/2 + x) = -cot x
- cot (π/2 + x) = -tan x
3. Công thức nhân
Nhân đôi:
- sin2a = 2sina.cosa
- cos2a = cos2a – sin2a = 2cos2a – 1 = 1 – 2sin2a
Nhân ba:
- sin3a = 3sina – 4sin3a
- cos3a = 4cos3a – 3cosa
Nhân bốn:
- sin4a = 4.sina.cos3a – 4.cosa.sin3a
- cos4a = 8.cos4a – 8.cos2a + 1
- hoặc cos4a = 8.sin4a – 8.sin2a + 1
4. Công thức hạ bậc
Được biến đổi từ công thức lượng giác cơ bản, cụ thể: sin2a=1 – cos2a = 1 – (cos2a + 1)/2 = (1 – cos2a)/2.
5. Công thức biến tổng thành tích
Mẹo ghi nhớ: cos + cos = 2 cos cos, cos – cos = – 2 sin sin, sin + sin = 2 sin cos, sin – sin = 2 cos sin.
Mẹo học thuộc công thức lượng giác nhanh chóng nhất
Công thức lượng giác dù quan trọng nhưng rất khó để có thể học thuộc. Do đó, các thầy cô giáo thường cung cấp cho học sinh những cách học thuộc lòng bảng công thức nhanh chóng và đơn giản nhất cho học sinh.
Một số mẹo học thuộc lòng bạn có thể tham khảo đó là:
1. Học thuộc công thức cộng lượng giác
Cos + cos = 2 cos cos/ Cos – cos = – 2 sin sin/ Sin + sin = 2 sin cos/ Sin – sin = 2 cos sin/ Sin thì sin cos cos sin/ Cos thì cos cos sin sin -/ Tang tổng lấy tổng tang/ Chia một trừ với tích tang.
2. Học thuộc công thức lượng giác đặc biệt
- Cos đối, sin bù, phụ chéo, khác tan.
- Cosin của 2 góc đối thì bằng nhau, sin của 2 góc bù nhau bằng nhau, nếu phụ chéo là 2 góc phụ nhau => sin góc này = cos góc kia, tan góc này = cot góc kia; tan của 2 góc hơn kém pi.
3. Học thuộc công thức lượng giác nhân ba
Nhân ba một góc bất kỳ, sin thì ba bốn, cos thì bốn ba.
4. Học thuộc công thức lượng giác gấp đôi
- Sin gấp đôi = 2 sin cos
- Cos gấp đôi = bình phương cos trừ bình phương sin = trừ 1 + 2 lần bình cos = +1 trừ 2 lần bình sin.
- Tang gấp đôi lấy đôi tang, chia 1 trừ lại bình tang ra liền.
5. Học thuộc công thức lượng giác biến đổi tổng thành tích nhanh chóng
- Sin tổng lập tổng sin cô/ Cô tổng lập hiệu đôi cô đôi chàng/ Tan tử là + đôi tan/ Một trừ tan tích mẫu mang thương sầu/ Gặp hiệu ta chớ lo âu / Đổi trừ thành + ghi sâu vào lòng.
6. Học thuộc công thức lượng giác biến đổi tích thành tổng
Cos cos nửa cos -+, +cos – trừ/ Sin sin nửa cos – trừ trừ cos +/ Sin cos nửa sin -+ +sin- trừ.
Trên đây là toàn bộ những công thức lượng giác từ cơ bản tới nâng cao mà bạn có thể tham khảo. Những công thức này sẽ theo các em học sinh xuyên suốt năm THPT. Vì vậy việc học thuộc là rất cần thiết để chinh phục các kỳ thi quan trọng, đạt thành tích cao. Hy vọng bài viết đã giúp ích cho bạn. Nếu có nhu cầu tham khảo thêm thông tin bổ ích khác, đừng quên truy cập vào website của chúng tôi nhé.