Hình tam giác là loại hình học thường gặp trong quá trình Toán Học. Loại hình này thường có nhiều kiểu khác nhau như tam giác đều, tam giác vuông, tam giác cân… Trong đó tam giác đều là loại có đặc trưng riêng biệt nhất với ba cạnh đều bằng nhau.
Bài viết này Wikikienthuc sẽ chia sẻ cho các bạn một số thông tin về tam giác đều và công thức tính diện tích tam giác đều.
Nội dung chính:
Tam giác đều là gì?
Tam giác đều là tam giác có 3 cạnh bằng nhau. Dấu hiệu nhận biết tam giác đều sẽ gồm:
- tam giác có ba cạnh bằng nhau;
- tam giác có ba góc bằng nhau;
- tam giác cân có một góc bằng 60 độ là tam giác đều
- tam giác có hai góc bằng 60 độ là tam giác đều
Tính chất của tam giác đều bao gồm:
- Trong một tam giác đều mỗi góc sẽ có 60 độ
- Nếu một tam giác có ba cạnh bằng nhau thì đó được gọi là tam giác đều
- Nếu một tam giác có một góc bằng 60 độ thì được gọi là tam giác đều
- Trong tam giác đều, đường trung tuyến của loại tam giác đều sẽ là đường cao và đường phân giác của tam giác đó
- Tam giác ABC đều có AD là đường trung tuyến kẻ từ đỉnh A và AD là đường cao và đường phân giác
Công thức tính diện tích tam giác đều
Giống như nhiều loại tam giác khác, tam giác đều được tính diện tích khá đơn giản.
Theo đó, công thức tính diện tích tam giác đều như sau: Diện tích tam giác đều bằng độ dài chiều cao nhân với cạnh đáy được bao nhiêu chia cho 2.
Cụ thể công thức: S = (a x h)/2
Trong đó:
- A là chiều dài của đáy tam giác đều (đáy là một trong 3 cạnh của tam giác)
- h là chiều cao của tam giác đều (chiều cao tam giác được tính bằng đoạn thẳng hạ từ đỉnh xuống đáy).
Lưu ý:
- Tam giác đều nên đường cao kẻ từ đỉnh A sẽ trùng với đường trung tuyến kẻ từ đỉnh.
- Khi tính diện tích tam giác thì chiều cao nào ứng với đáy đó
- Nếu hai tam giác có chung chiều cao hoặc chiều cao bằng nhau thì diện tích của hai tam giác đó tỉ lệ với 2 cạnh đáy và ngược lại.
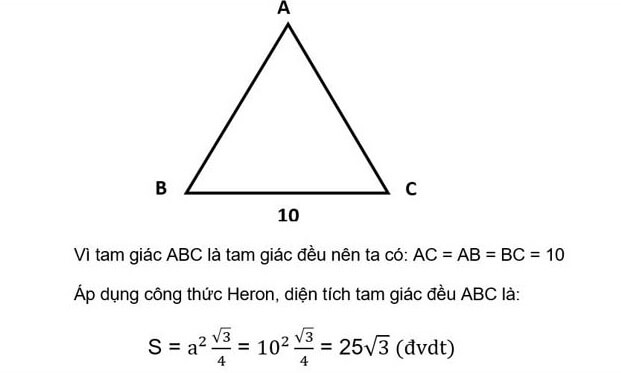
Ngoài công thức trên, các bạn có thể áp dụng thêm công thức Heron để tính diện tích tam giác đều. Công thức sẽ được tính bằng bình phương độ dài các cạnh của tam giác đều nhân với căn bậc 2 của 3 chia cho 4. Công thức: S = a2. √3/4
Nếu tam giác đều cao kẻ từ đỉnh A trùng với đường trung tuyến kẻ đỉnh A của tam giác ABC. Thì chúng ta có thể áp dụng công thức tính diện tích tam giác ABC là: S = AH*BC/2
Bài tập áp dụng tính diện tích tam giác đều
Bài tập tính diện tích tam giác đều cực kỳ đa dạng. Mỗi kiểu sẽ có một cách giải khác nhau, vì thế cần phải chú ý để thực hiện đúng theo yêu cầu của công thức. Dưới đây là một số kiểu bài tập tiêu biểu mà bạn có thể chú ý để áp dụng:
Tính diện tích tam giác đều ABC ngoại tiếp đường tròn (I, r)
Cách giải:
Gọi H là tiếp tuyến của đường tròn (I) với BC.
Chúng ta có: (IH perp BC ) (thuộc tính tiếp tuyến)
Vì I là tâm của đường tròn nội tiếp tam giác ABC nên AI là tia phân giác của ( widehat {BAC} )
Tam giác (ABC ) đều nên AI cũng là đường cao của ( bigtriangleup ABC ). Khi đó A, I, H thẳng hàng.
Ta có: (HB = HC ) (tính chất tam giác đều)
Tam giác (ABC ) đều nên I cũng là tâm của ( bigtriangleup ABC ).
Suy ra: (AH = 3.HI = 3.r )
Tính chiều cao của hình tam giác có độ dài cạnh đáy bằng 50cm và diện tích bằng 1125cm2.
Cách giải: Chiều cao của hình tam giác là: 1125 x 2 : 50 = 45 (cm)
Đáp số: 45cm
Một hình tam giác có đáy 12cm và chiều cao 25mm. Tính diện tích hình tam giác đó?
Cách giải: Đổi: 25mm = 2,5 cm
Diện tích hình tam giác đó là: 12 x 2,5 : 2 = 15 (cm2)
Đáp số: 15cm2
Một tấm bảng quảng cáo hình tam giác có tổng cạnh đáy và chiều cao là 28m, cạnh đáy hơn chiều cao 12m. Tính diện tích tấm bảng quảng cáo đó?
Cách giải:
Độ dài cạnh đáy là: (28 + 12) : 2 = 20 (m)
Độ dài chiều cao là: 28 – 20 = 8 (m)
Diện tích tấm bảng quảng cáo là: 20 x 8 : 2 = 80 (m2)
Đáp số: 80m2
Ứng dụng của tam giác đều trong đời sống
Tam giác đều là một loai tam giác khá phổ biến trong đời sống hiện nay. Có thể thấy, tam giác đều được ứng dụng nhiều trong các lĩnh vực.
- Tam giác đều được ứng dụng trong việc làm đồ chơi cho trẻ em;
- Giúp tạo nên các mô hình trong học tập cho học sinh;
- Ứng dụng để đo chiều cao của vật như tòa nhà, tháp, cây,…
Bước 1: Tiến hành đo đạc bằng cách đặt cọc AB thẳng đứng từ trên xuống. Ở phía trên có gắn thước ngắm quay được đặt quanh một cái chốt của cọc. Sau đó điều khiển phần thước ngắm sao cho có hướng thước đi thẳng qua đỉnh B’ của vật và xác định giao điểm của đường thẳng BB’ và AA’.
Bước 2: Tính chiều cao của vật
- Có thể đo khoảng cách giữa hai địa điểm trong đó có một số địa điểm không thể tới được sẽ áp dụng công thức này;
Tam giác đều mang khá nhiều đặc điểm nổi bật trong công thức và tính chất. Với những giới thiệu trên của chúng tôi, hy vọng rằng bạn đọc đã phần nào hiểu rõ hơn về loại tam giác này. Tiếp tục theo dõi bài viết để tìm kiếm những thông tin hay ho khác nhé.