Trong toán học, hệ thức lượng trong tam giác là nội dung kiến thức cơ bản vô cùng quan trọng trong quá trình học tập của học sinh, sinh viên. Hơn hết, nếu bạn theo đuổi lĩnh vực xây dựng – thiết kế. Hệ thức lượng còn được áp dụng trong việc tính toán kích thước phòng ở, không gian…
Trong bài viết dưới đây, hãy cùng Wikikienthuc chúng ta cùng đi tìm hiểu những công thức liên quan đến hệ thức lượng trong tam giác vuông cân nhé.
Nội dung chính:
Kiến thức cơ bản về hình tam giác
Tiến đến tiếp đến những kiến thức cơ bản về hệ thức lượng, người học cần nắm được định nghĩa và tính chất của hình tam giác.
1. Hình tam giác là gì?
Theo đó, tam giác là một hình cơ bản, phổ biến trong toán học, được cấu thành bởi ba điểm không thẳng hàng, có 3 cạnh cũng là ba đoạn thẳng nối các đỉnh với nhau. Tam giác được coi là một đa dạng đơn, đồng thời là đa giác có số cạnh ít nhất, chỉ với 3 cạnh.
Có một số loại tam giác đặc biệt như tam giác cân, tam giác vuông, tam giác vuông cân, tam giác đều.
2. Tính chất của hình tam giác
Một số tính chất của hình tam giác có thể kể đến như sau:
- Tam giác có 3 đỉnh, 3 cạnh, 3 góc.
- Tổng ba góc trong một trong tam giác bằng 180 độ.
- Các góc trong của một tam giác được gọi là góc trong.
- Trong tam giác còn có góc ngoài, là góc kề bù với góc trong.
- Số đo góc ngoài được tính bằng tổng các góc trong không kề bù với nó. Trong tam giác, có 3 góc trong, 6 góc ngoài.
Quy ước về các ký hiệu trong hình tam giác
Để nắm được công thức một cách chính xác nhất, cần biết những quy ước về ký hiệu trong tam giác được sử dụng trong hệ thức lượng.
- Ký hiệu a, b, c là độ dài các cạnh đối diện, tương đương với 3 đỉnh A, B, C trong tam giác.
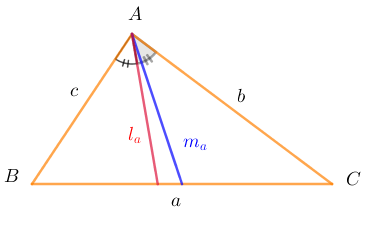
- ha, hb, hc là độ dài đường cao xuất phát từ 3 đỉnh A, B, C.
- ma, mb, mc là độ dài đường trung tuyến xuất phát từ 3 đỉnh A, B, C.
- la, lb, lc là độ dài các đường phân giác xuất phát từ 3 đỉnh A, B, C.
- S là diện tích hình tam giác.
- R là bán kính đường tròn nội tiếp.
- r là bán kính đường tròn ngoại tiếp.
- P là chu vi hình tam giác.
Hệ thức lượng trong tam giác
Hệ thức lượng trong tam giác là công thức liên hệ giữa các cạnh, các góc trong một tam giác đã được nghiên cứu và đưa vào sử dụng. Theo đó, có hệ thức lượng trong tam giác thường và hệ thức lượng trong tam giác đặc biệt – tam giác vuông.
1. Hệ thức lượng trong tam giác thường
Trong tam giác thường, phổ biến nhất là định lượng cosin và định lý sin. Cụ thể như sau.
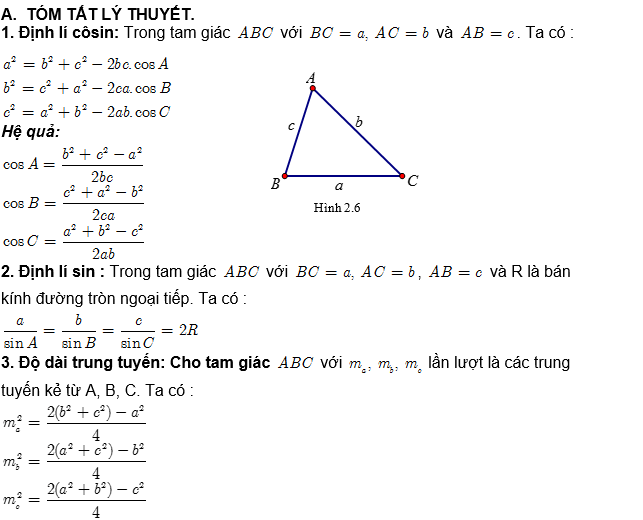
1. Định lý cosin
Định lí: Trong một tam giác bất kì, bình phương một cạnh bằng tổng các bình phương của hai cạnh còn lại trừ đi hai lần tích của hai cạnh đó nhân với Cosin của góc xen giữa chúng.

2. Định lý sin
Định lí: Trong tam giác ABC bất kỳ, tỉ số giữa một cạnh và sin của góc đối diện với cạnh đó bằng đường kính của đường tròn ngoại tiếp tam giác, nghĩa là.
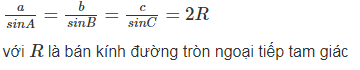
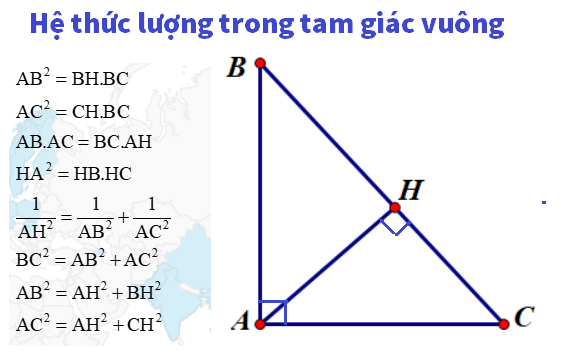
2. Hệ thức lượng trong tam giác vuông
Bên cạnh hệ thức lượng trong tam giác thường, còn có những trường hợp đặc biệt khi ứng dụng hệ thức lượng trong tam giác vuông. Các công thức này liên quan đến độ dài các cạnh, chiều cao trong tam giác. Xét tam giác ABC vuông tại A, có đường cao AH, AH = h, ta có các hệ thức lượng trong tam giác vuông cụ thể như sau:
- a x a = b x b + c x c
- b x c = a x h (trong đó, h là độ dài chiều cao xuất phát từ đỉnh A của tam giác ABC vuông tại A)
- 1/(h x h) = 1/ (b x b) + 1/ (c x c) (h là độ dài chiều cao xuất phát từ đỉnh A của tam giác ABC vuông tại A)
a. Tỉ số lượng giác của góc nhọn
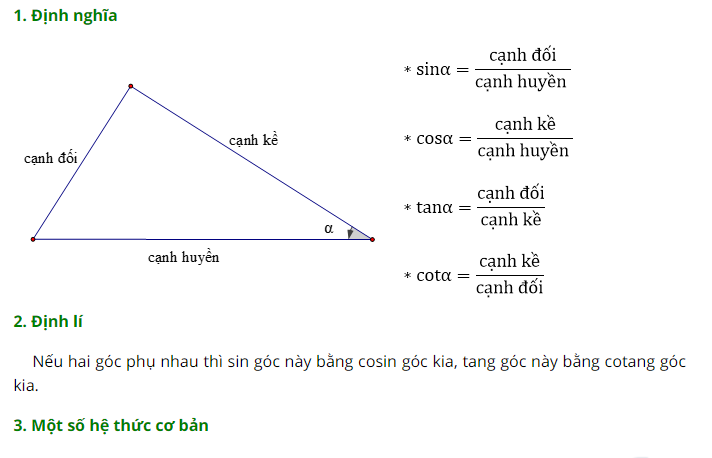
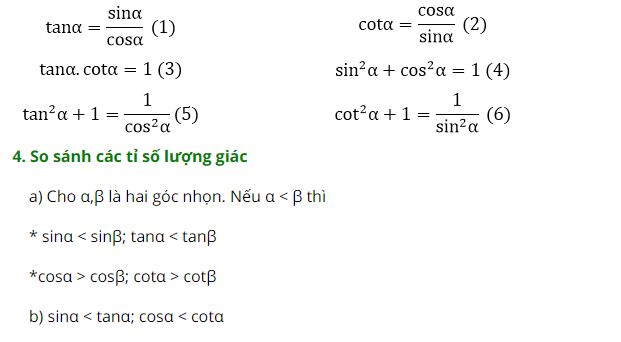
b. Hệ thức về góc và cạnh trong tam giác vuông
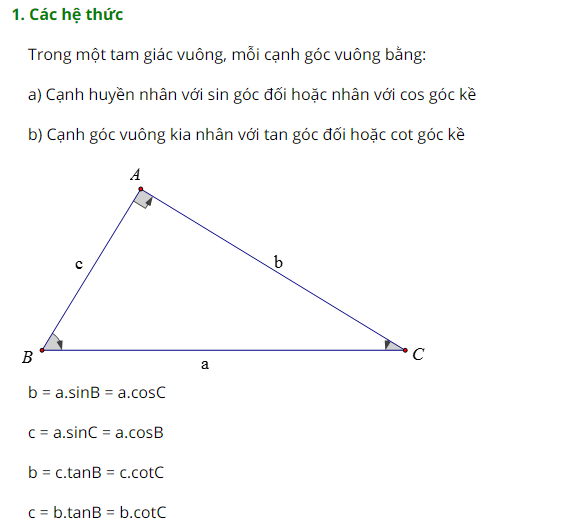
Hệ thức lượng trong tam giác thường và hệ thức lượng trong tam giác vuông – một trường hợp đặc biệt có tính ứng dụng cao. Chúng sử dụng trong nhiều dạng toán tính toán số đo góc, số đo cạnh, diện tích, chu vi tam giác,…
Trên đây là bài viết của chúng tôi về hệ thức lượng trong tam giác. Không thể phủ nhận, đây là một kiến thức cơ bản, được ứng dụng để giải quyết nhiều dạng toán khác nhau. Bởi vậy, nắm chắc các kiến thức về hệ thức lượng là tiền đề rất quan trọng để tiến tới học nâng cao và giải quyết nhiều môn học trong tương lai.