Hình thang cân là một kiến thức hình học quan trọng trong toán học lớp 8. Để chứng minh được tứ giác là hình thang cân bạn cần nắm vững được định nghĩa, tính chất và dấu hiệu nhận biết. Vậy bạn đã biết cách chứng minh tứ giác ABCD là hình thang cân nhanh, chính xác chưa? hãy tham khảo bài viết dưới đây của chúng tôi để có thêm nhiều thông tin hữu ích nhé!
Nội dung chính:
Định nghĩa hình thang cân
Hình thang là tứ giác có một cặp cạnh đối song song với nhau, hai cạnh này được gọi là cạnh đáy của hình thang, hai cạnh còn lại được gọi là 2 cạnh bên.
Hình thang cân là hình thang có hai góc kề một đáy bằng nhau.
Tứ giác ABCD là hình thang cân có cạnh đáy AB,CD. Khi đó, ta có: góc ACD=BCD, hoặc góc DAB= CBA.
Tính chất hình thang cân
Hình thang cân sẽ có tất cả các tính chất của hình thang, đồng thời có thêm một số tính chất đặc biệt dưới đây:
- Trong hình thang cân hai cạnh bên bằng nhau: Hình thang ABCD cân (AB//CD) suy ra : AD=BC
- Trong hình thang cân hai góc kề cạnh đáy bằng nhau: Hình thang ABCD cân (AB//CD) suy ra: góc ADC=góc BCD và góc DAB=góc ABC.
- Trong hình thang cân hai đường chéo bằng nhau: Hình thang ABCD cân (AB//CD) suy ra: AC=BD
- Hình thang cân là tứ giác nội tiếp đường tròn.
Dấu hiệu nhận biết hình thang cân
Dưới đây là các dấu hiệu nhận biết hình thang cân bạn nên nắm vững:
- Hình thang có hai góc kề một đáy bằng nhau là hình thang cân ( theo định nghĩa hình thang cân).
- Hình thang có hai đường chéo bằng nhau là hình thang cân (theo tính chất hình thang cân).
Lưu ý: Hình thang cân thì hai cạnh bên sẽ bằng nhau, tuy nhiên hình thang có hai cạnh bên bằng nhau thì chưa chắc là hình thang cân. Ví dụ như hình bình hành ABCD có AB//CD, AC=BD đây là hình thang nhưng không phải là hình thang cân.
- Hình thang nội tiếp đường tròn là hình thang cân (theo tính chất hình thang cân).
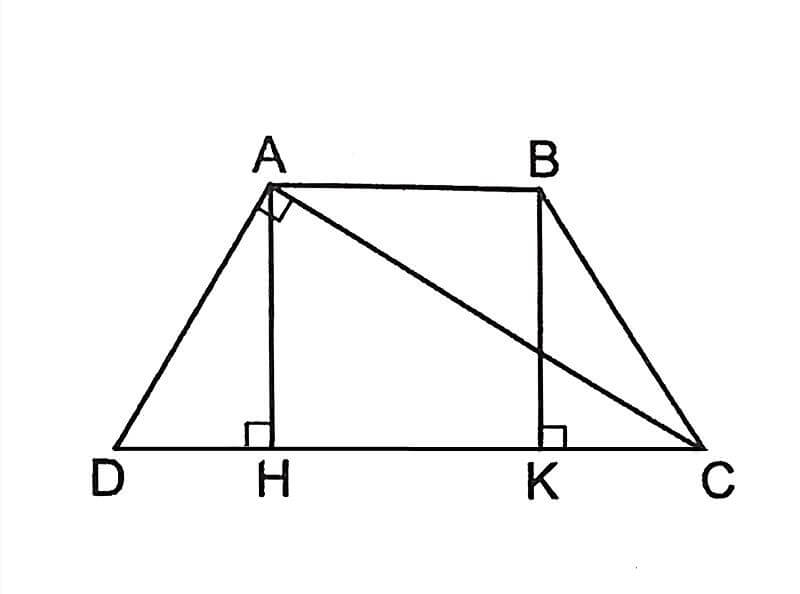
Cách tính diện tích hình thang cân
Cách tính diện tích hình thang cân áp dụng công thức tính diện tích hình thang như thông thường.
Diện tích hình thang/hình thang cân bằng chiều cao nhân với trung bình cộng của hai cạnh đáy:
Hình thang cân ABCD (AB//CD) có AB=a, CD=b, AH=h.
Khi đó diện tích hình thang ABCD là:
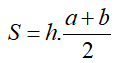
Mẹo học thuộc công thức tính diện tích hình thang cân:
“ Muốn tính diện tích hình thang
Đáy lớn, đáy bé ta đem cộng vào
Cộng vào nhân với chiều cao
Chia đôi kết quả thế nào cũng ra”
Cách tính chu vi hình thang cân
Hình thang cân ABCD (Ab//CD) có độ dài cạnh đáy AB, CD lần lượt là a,b; độ dài 2 cạnh bên AD, BC bằng c.
Khi đó, chu vi hình thang cân ABCD là: P= a+b+2c
Cách chứng minh hình thang cân
Các bài toán liên quan đến chứng minh hình thang cân sẽ có 2 dạng chính dưới đây:
Dạng 1: Chứng minh hình thang là hình thang cân
- Chứng minh hình thang có 2 cạnh kề 1 đáy bằng nhau là hình thang cân.
- Chứng minh hình thang có 2 đường chéo bằng nhau là hình thang cân.
Bài toán minh họa:
Hình thang ABCD (AB//CD) có góc ACD= góc BDC. chứng minh tứ giác ABCD là hình thang cân.
Lời giải:
Gọi E là giao điểm của AC và BD
Xét tam giác EDC ta có:
góc EDC= góc ECD ( giả thiết)
=> tam giác EDC cân tại E
Suy ra: ED=EC (1)
Theo bài ra ta có: AB//CD
=> góc CAB = góc ACD (2 góc so le ) và góc ABD= góc BDC
Mà góc ADC= góc BDC ( giả thiết)
Suy ra: góc CAB= góc DBA
Tương tự ta chứng minh được tam giác EAB cân tại E
=> EA= EB (2)
Từ (1) và (2) suy ra: AE+EC= BE+ED
Tương đương AC=BD
Hình thang ABCD có hai cạnh chéo bằng nhau nên đây là hình thang cân (đpcm).
Dạng 2: Chứng minh tứ giác là hình thang cân
Bước 1: Chứng minh tứ giác là hình thang. Để chứng minh tứ giác là hình thang bạn cần 2 cạnh trong tứ giác song song với nhau, dựa vào: hai góc vị trí đồng vị bằng nhau, hai góc vị trí song song bằng nhau, hai góc cùng phía bù nhau nhau hoặc định lý từ góc vuông đến song song.
Bước 2: Chứng minh hình thang là hình thang cân.
Bài toán minh họa:
Cho tam giác ABC cân tại A, các đường phân giác BD, CE ( D thuộc AC, E thuộc AB). Chứng minh tứ giác ABCD là hình thang cân.
Theo bài ra ta có tam giác ABC cân tại A
=> góc ABC = góc ACB
Mà BD, CE lần lượt là tia phân giác của góc ABC và góc ACB
=> góc B1=B2=C1=C2
Dễ dàng chứng minh được tam giác ABD= tam giác ACE (g.c.g)
=>AD=AE (2 cạnh tương ứng)
Xét tam giác ADE ta có:
^AED+ ^ADE + ^A= 180 độ ( định lý tổng 3 góc trong tam giác)
=> 2 ^AED + ^A=180 độ
=> ^AED= (180 độ -^A)/2 (1)
Tương tự, xét tam giác ABC ta có:
^ABC + ^ACB + ^A= 180 độ
=> ^ABC = (180- ^A)/2 (2)
Từ (1), (2) => ^AED=^ABC
Mà 2 góc này ở vị trí đồng vị nên suy ra ED//BC
=> tứ giác EDBC là hình thang
Mặt khác ^EBC=^ DCB (giả thiết)
=> EDBC là hình thang cân
Trên đây là toàn bộ nội dung tìm hiểu về định nghĩa, tính chất, dấu hiệu nhận biết hình thang cân. Hy vọng những thông tin hữu ích của bài viết sẽ giúp bạn đọc hoàn thành tốt các bài toán liên quan đến hình thang và hình thang cân. Để có thêm nhiều thông tin thu vị khác, hãy truy cập vào website của chúng tôi nhé.